41. Найдите cos(x - у), если: 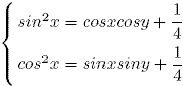
|
|
A) |
√3/2 |
B) |
1 |
C) |
1/2 |
D) |
√2/2 |
| |
Правильный ответ:
|
C |
| |
Решение: |
Сложим левую часть первого уравнения с левой частью второй, а правую часть первого уравнения с правой частью второй: sin2x + cos2x = cosxcosy + 1/4 + sinxsiny + 1/4. Применим формулы: sin2x + cos2x = 1 cos(α - β) = cosα cosβ + sinα sinβ Получаем: 1 = cos(x - y) + 2/4 = cos(x - y) + 1/2. cos(x - y) = 1 - 1/2 = 1/2. Дополнительный комментарий: При переносе слагаемого из одной части уравнения в другую знак меняется на противоположный: • х + 1 = 4; переносим 1 вправо со знаком минус: х = 4 - 1. • x - 1 = 4; переносим -1 вправо со знаком плюс: х = 4 + 1. • 1 = cos(x - y) + 1/2; переносим 1/2 влево со знаком минус: 1 - 1/2 = cos(x - y). |
| |
Категория: |
Тригонометрия |
|
В начало | Предыдущий | Следующий
|