Дифференцируемая функция F(x) называется первообразной от функции f(x) на данном промежутке, если для всех значений х из этого промежутка справедливо равенство: F`(x) = f(x).

Интеграл от функции f(x) на отрезке [a; b] является разностью первообразных F(b) - F(a). Числа a и b называются пределами интегрирования (a - нижним пределом, b - верхним). Формула Ньютона-Лейбница: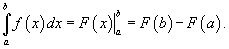

В данном случае нужно найти интеграл на отрезке [0; π], т.е. F(π) - F(0).

1) Для нахождения первообразной F(x) применим формулу:

1) ∫sinxdx = -cosx.

Учитываем, что если в сложных функциях перед x есть коэффициент k, то перед первообразной функцией появляется 1/k. В данном случае коэффициент k = 1/2, значит перед функцией появляется 1/k = 2.

Получаем:

∫sin(x/2)dx = 2*(-cos(x/2)) = -2cos(x/2).

2) Подставим вместо х значения 0 и π, согласно формуле Ньютона-Лейбница:

-2*(cos(π/2) - cos0) = -2*(0 - 1) = -2*(-1) = 2.