Дифференцируемая функция F(x) называется первообразной от функции f(x) на данном промежутке, если для всех значений х из этого промежутка справедливо равенство: F`(x) = f(x). В данном случае нужно найти первообразную F(x). 1) Применим формулу: ∫xndx = (xn+1)/(n+1). Запишем дробь  в виде отрицательной степени х-2/3. в виде отрицательной степени х-2/3. Получаем: (х-2/3 + 1) / (-2/3 + 1) = х1/3 : 1/3 = 3х1/3. 2) Учитываем, что если k и b являются постоянными величинами, то для f(kx + b) первообразной будет 1/k*F(kx + b), т.е. k выносится вперед в виде 1/k. Найдем первообразную от (2х - 3)2: 1/2*(2х - 3)2+1 / (2+1) = 1/2*((2х - 3)3 / 3 = 1/6*(2х - 3)3. 3) Так как график функции проходит через точку (1; 1/6), т.е. х = 1, F(x) = 1/6, можно найти значение С: 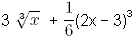 + C = 1/6. + C = 1/6.
3 + 1/6 * (2 - 3)3 + C = 1/6. 3 - 1/6 + C = 1/6. C = 1/6 - 2 5/6 = -2 4/6 = -2 2/3. Таким образом, правильный ответ: 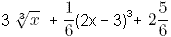 Способ немного попроще: Так как известны значения х и F(x), то можно сразу подставить их во все ответы поочередно, например: 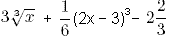 = 1/6. = 1/6.
3 + 1/6 * (2 - 3)3 - 2 2/3 = 3 - 1/6 - 2 4/6 = 3 - 2 5/6 = 1/6. Как видно, ответ верный. |