38. Дана арифметическая прогрессия a1,а2,...,аn (d≠0). Какие из следующих чисел составляют арифметическую прогрессию? 1) a1, a3, a5, ..., a2n-1; 2) √a2, √a4, √a6, ..., √a2n; 3) a1+a2, a2+a3, a3+a4, ..., a2n-1+a2n; 4) a1+a3, a3+a5, a5+a7, ..., a2n-3+a2n-1; 5) 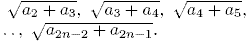 |
Арифметическая прогрессия - это числовая последовательность, у которой задан первый член a1, а каждый следующий член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d. Возьмем любую арифметическую прогрессию, например: 1,4,7,10,13,16,19,... 1) 1,7,13,... - является арифметической прогрессией, при d = 6. 3) 1+4,4+7,7+10,... или 5,11,17 - является арифметической прогрессией при d = 6. 4) 1+7, 7+13, 13+19,... или 8,20,32 - является арифметической прогрессией при d = 12. Арифметическая прогрессия никогда не получается из квадратных корней. Таким образом, не составляют арифметическую прогрессию 1,3,4. |