Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называются боковыми, а третья сторона называется основанием треугольника. У равнобедренного треугольника углы при основании равны. Высота треугольника — это отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне. В данном случае высота AH опущена на боковую сторону ВС: 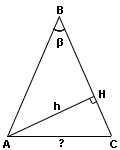
В равнобедренном треугольнике АВС: - стороны АВ и ВС равны между собой (АВ = ВС), т.к. являются боковым сторонами; - углы ∠А и ∠С тоже равны между собой (∠А = ∠С), т.к. являются углами при основании; - АН является высотой, опущенной к боковой стороне ВС, поэтому ∠АНВ = ∠АНС = 90°. По условию задачи: - ∠В = β; - АН = h; - AC = ?. В треугольнике АНС: - ∠С = (180° - β) : 2 = 90° - β/2; - катет АН = h; - AC является гипотенузой. Так как синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, то получаем: sinC = AH / АС. sin(90° - β/2) = h/AC. По формуле приведения: sin(90° – α) = cosα Получаем: sin(90° - β/2) = cos(β/2). Следовательно: cos(β/2) = h/AC. AC = 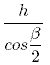 |