Периметр - это сумма длин всех сторон многоугольника (треугольника, квадрата, прямоугольника и т.д.).

Высота треугольника — это отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.

В данном случае обозначим стороны полученных двух треугольников буквами a, b, m и n.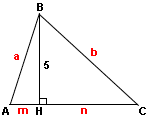

Нужно найти периметр АВС, т.е.:

a + b + m + n = ?

Так как по условию периметр первого из полученных треугольников равен 18, то получаем:

a + m + 5 = 18.

a + m = 18 - 5 = 13.

Периметр второго треугольника равен 26:

b + n + 5 = 26.

b + n = 26 - 5 = 21.

Следовательно:

a + b + m + n = (a + m) + (b + n) = 13 + 21 = 34.