Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называются боковыми, а третья сторона называется основанием треугольника. У равнобедренного треугольника углы при основании равны.

Высота треугольника — это отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.

В данном случае высота BD опущена на основание АС: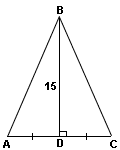

Обозначим основание АС за х. Тогда боковая сторона составит (х - 15), т.к. по условию она меньше основания на 15.

Так как высота BD перпендикулярна основанию АС, то образуются прямоугольные треугольники ABD и CBD. Причем AD = CD = х/2, т.к. высота в равнобедренном треугольнике является медианой, т.е. делит сторону пополам.

Следовательно, в прямоугольном треугольнике CBD гипотенузой является сторона ВС, катетами являются стороны BD и СВ.

Воспользуемся теоремой Пифагора, по которой сумма квадратов катетов равна квадрату гипотенузы:

ВС² = BD² + CB².

(x - 15)² = 15² + (x/2)².

x² - 30x + 225 = 225 + x²/4.

х² - 30х = х²/4.

Умножим обе части уравнения на 4, чтобы избавиться от знаменателя:

4х² - 120х = х².

Перенесем все слагаемые в одну сторону:

4х² - х² - 120х = 0.

3х² - 120х = 0.

Разделим обе части уравнения на 3 для упрощения расчетов:

х² - 40х = 0.

Вынесем х за скобки:

х·(х - 40) = 0.

Произведение равно нулю, если хотя бы один из множителей равен нулю, а остальные имеют смысл.

В данном случае х = 0 или х = 40.

Так как х = 0 не подходит (сторона не может быть 0), то остается вариант х = 40.

Таким образом, основание треугольника составляет 40.