Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называются боковыми, а третья сторона называется основанием треугольника. У равнобедренного треугольника углы при основании равны.

Высота треугольника — это отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.

В данном случае высота опущена на боковую сторону ВС: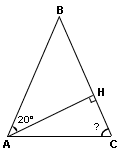

В равнобедренном треугольнике АВС:

- стороны АВ и ВС равны между собой (АВ = ВС), т.к. являются боковым сторонами;

- углы ∠А и ∠С тоже равны между собой (∠А = ∠С), т.к. являются углами при основании;

- АН является высотой, опущенной к боковой стороне ВС.

В прямоугольном треугольнике АВН:

- ∠А = 20°;

- ∠Н = 90°;

- ∠В = 180° - 20° - 90° = 70° (т.к. сумма внутренних углов треугольника составляет 180 градусов).

Таким образом, угол ∠В при вершине треугольника АВС равен 70°.

Так как углы при основании равнобедренного треугольника равны между собой, а сумма всех внутренних углов треугольника составляет 180°, то угол при основании находим следующим образом:

∠C = ∠А = (180° - 70°) : 2 = 110° : 2 = 55°.