Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называются боковыми, а третья сторона называется основанием треугольника. У равнобедренного треугольника углы при основании равны.

Биссектриса треугольника - это отрезок, соединяющий вершину угла с точкой на противоположной стороне треугольника и делящий этот угол пополам.

В данном случае: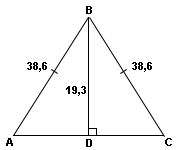

АВ = ВС = 38,6, т.к. у равнобедренного треугольника боковые стороны равны между собой.

∠А = ∠С, т.к. углы при основании равнобедренного треугольника тоже равны между собой.

По условию BD является высотой, проведенной к основанию треугольника.

Образуется новый прямоугольный треугольник ABD, в котором:

∠D = 90°;

катет BD ровно в два раза меньше гипотенузы AB (38,6 : 19,3 = 2).

Следовательно, угол ∠А = 30°, т.к. катет, лежащий против угла 30°, равен половине длины гипотенузы.

Таким образом, ∠А = ∠С = 30°.

Проведем две биссектрисы АЕ и CF из углов при основании.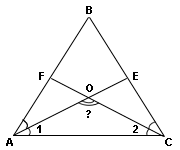

Так как биссектрисы делят углы ∠А и ∠С пополам, то углы ∠1 и ∠2 составят по 15° (30° : 2 = 15°).

Сумма углов треугольника равна 180°.

Следовательно, искомый тупой угол между биссектрисами ∠AOD составит:

180° - 15° - 15° = 150°.