Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называются боковыми, а третья сторона называется основанием треугольника. У равнобедренного треугольника углы при основании равны.

Биссектриса треугольника - это отрезок, соединяющий вершину угла с точкой на противоположной стороне треугольника и делящий этот угол пополам.

В данном случае: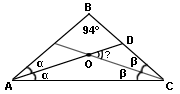

АВ = ВС, т.к. являются боковыми сторонами равнобедренного треугольника.

∠А = ∠С, т.к. являются углами при основании равнобедренного треугольника.

Так как по условию ∠В = 94°, а сумма всех внутренних углов треугольника 180°, то оставшиеся ∠А и ∠С в сумме составляют 180° - 94° = 86°.

Учитывая, что ∠А = ∠С, каждый из них равен 86° : 2 = 43°.

По условию углы при основании делятся биссектрисой пополам, поэтому каждый из полученных углов составит 43°/2. Обозначим их α и β:

α = 43°/2;

β = 43°/2);

α + β = 43°.

Искомый угол ∠DOC является внешним углом треугольника АОС.

Так как внешний угол равен сумме двух внутренних углов с ним не смежных, то ∠DOC = α + β = 43°.