49. Один из внутренних односторонних углов при параллельных прямых и секущей на 60° меньше другого. Найдите больший из этих углов. |
|
A) |
110° |
B) |
130° |
C) |
118° |
D) |
120° |
| |
Правильный ответ:
|
D |
| |
Решение: |
Сумма внутренних односторонних углов при пересечении двух параллельных прямых третьей прямой (секущей) равна 180°. В данном случае углы 1 и 2 являются внутренними односторонними углами. 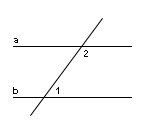
Если принять больший из углов за х, то второй составит (х - 60°), т.к. по условию он на 60° меньше первого. Получается уравнение: х + (х - 60°) = 180°. 2х - 60° = 180°. 2х = 180° + 60° = 240°. х = 240° : 2 = 120°. Как видно, больший из углов равен 120°. |
| |
Категория: |
Геометрия |
|
В начало | Предыдущий | Следующий
|