Равнобедренный треугольник - это треугольник, у которого две стороны равны. Равные стороны называются боковыми, а третья сторона называется основанием. Углы при основании равнобедренного треугольника равны.

Биссектриса треугольника - это отрезок, который делит угол пополам и соединяет вершину угла с точкой на противолежащей стороне.

В данном случае: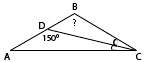

∠А = ∠С, т.к. это углы при основании.

Так как биссектриса CD делит угол ∠C пополам, то ∠ACD = ∠BCD. Обозначим каждый из этих углов за х.

Следовательно, ∠А = ∠С = 2х.

Таким образом, в треугольнике ADC имеем следующее:

∠А = 2х,

∠С = х,

∠D = 150°.

Так как сумма углов треугольника составляет 180°, то получаем уравнение:

2х + х + 150° = 180°.

3х = 180° - 150° = 30°.

х = 30° : 3 = 10°.

Как видно: ∠А = 2·10° = 20°.

В треугольнике ABC известны:

∠А = ∠С = 20°.

Сумма этих углов 20° + 20° = 40°.

Вычитая сумму двух углов из 180°, найдем величину третьего угла ∠B:

180° - 40° = 140°.