Периметр - это сумма длин всех сторон многоугольника (треугольника, квадрата, прямоугольника и т.д.).

Медиана - это отрезок, который соединяет вершину треугольника с серединой противоположной стороны, т.е. делит эту сторону пополам.

В данном случае обозначим стороны полученных двух треугольников буквами a, m, а саму медиану - х.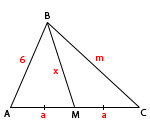

Нужно найти длину боковой стороны m (m = ?).

Так как медиана делит сторону пополам, то AM и MC равны между собой.

Периметр первого треугольника ABM равен 18:

a + 6 + x = 18.

a + x = 18 - 6 = 12.

Периметр второго треугольника BMC равен 24:

m + a + x = 24.

Вместо (a + x) подставляем ранее полученное значение 12:

m + 12 = 24.

m = 24 - 12 = 12.

Таким образом, длина большей боковой стороны составляет 12.