Длина окружности находится по формуле: C = 2πR В данном случае длина окружности составляет 18π√2. Следовательно: 2πR = 18π√2. 2R = 18√2. R = 9√2. Таким образом, радиус окружности равен 9√2 (АО = ВО = R = 9√2). 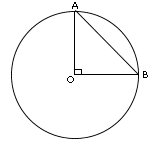
В треугольнике АОВ хорда АВ стягивает дугу в 90°. Так как ∠АОВ является центральным и измеряется дугой, на которую опирается, то его величина также 90°. Как видно, треугольник АОВ прямоугольный, где АВ - гипотенуза, АО и ВО - катеты. Чтобы найти гипотенузу, можно воспользоваться теоремой Пифагора. Либо учесть, что, если катеты в прямоугольном треугольнике равны между собой (например, каждый по х см), то гипотенуза находится по формуле х√2. В данном случае длина каждого из катетов АО = ВО = R = 9√2. Гипотенуза составит: 9√2 · √2 = 9√4 = 9·2 = 18. |