Площади подобных треугольников относятся как квадраты их периметров.

Следовательно, высказывание "площади подобных треугольников относятся как их периметры" - ложно.

Треугольник АВС - прямоугольный.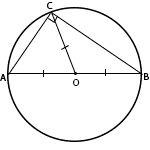

∠С - прямой (90°).

АВ - гипотенуза треугольника.

СО - медиана, которая делит гипотенузу пополам.

АО = ВО = СО = R (R - радиус описанной окружности).

Следовательно, высказываение "в прямоугольном треугольнике медиана, проведенная к гипотенузе, равна радиусу круга, описанного около этого треугольника" - верно.

ABCDEF - правильный шестиугольник, у которого все стороны равны между собой и равны радиусу описанной около него окружности.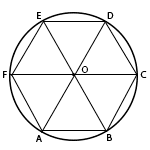

AD - бОльшая диагональ шестиугольника.

AD = AO + DO = R + R = 2R (R - радиус окружности).

Так как диаметр окружности в два раза больше радиуса, то бОльшая диагональ AD = 2R = диаметр окружности.

Следовательно, высказывание "в правильном шестиугольнике большая диагональ равна диаметру описанного около него круга" - верно.

ABC - правильный треугольник, у которого все стороны равны (он же равносторонний треугольник).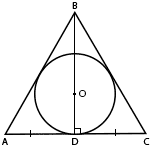

BD - медиана, которая делит сторону АС пополам.

О - центр вписанной окружности и точка пересечения всех трех медиан треугольника.

Так как точка пересечения медиан делит медиану в отношении 1:2, считая от вершины, то OD : OB = 1 : 2.

Следовательно, OD = 1/3 BD и, таким образом, высказывание "в правильном треугольнике 1/3 медианы равна радиусу круга, вписанного в этот треугольник" - верно.

Так как требуется указать ложное высказывание, то это "площади подобных треугольников относятся как их периметры".