Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

У прямоугольной трапеции два угла прямые, т.е. по 90°.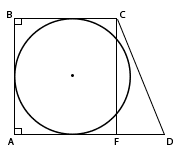

В данном случае:

∠А = ∠В = 90°.

ВС || AD.

БОльшая боковая сторона CD равна 2 см.

∠D = 30°.

Проведем перпендикуляр CF из точки С на сторону AD.

Так как трапеция прямоугольная, то AB перпендикулярно AD.

Следовательно, AB и CF параллельны (два перпендикуляра к одной прямой всегда параллельны).

Так как окружность вписана, то AB и CF являются диаметрами окружности и равны двум радиусам ( = 2R).

Длина окружности высчитывается по формуле:

C = 2πR.

Следовательно, нужно найти длину CF, которая равна, как указали выше, 2R.

В прямоугольном треугольнике CDF:

CD - гипотенуза, которая по условию задания равна 2 см.

∠D - острый угол, который равен 30°.

Так как известно, что катет, лежащий против угла в 30°, равен половине гипотенузы, то катет CF составит 2 : 2 = 1 см.

Таким образом, 2R = CF = 1 см.

Находим длину окружности по вышеупомянутой формуле:

C = 2πR = 1·π = π.