56. Наибольшее и наименьшее расстояния от точки, лежащей вне окружности, до окружности равны 6 и 2. Найдите длину окружности. |
|
A) |
4π |
B) |
π |
C) |
2π |
D) |
3π |
| |
Правильный ответ:
|
A |
| |
Решение: |
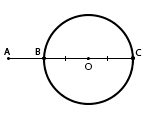
АС - наибольшее расстояние от точки А до окружности и равно 6. АВ - наименьшее расстояние от точки А до окружности и равно 2. О - центр окружности. ВО и СО - радиусы окружности. Так как АС = 6, АВ = 2, то ВС = 6 - 2 = 4. Следовательно, радиус окружности составляет 4 : 2 = 2 (ВО = СО = R = 2). Зная радиус, можно найти длину окружности по формуле: C = 2πR. В данном случае длина окружности: C = 2π·2 = 4π. |
| |
Категория: |
Геометрия |
|
В начало | Предыдущий | Следующий
|