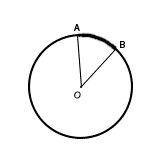
Радиус круга AO = BO = 5.

AOB - круговой сектор. Его дуга AB.

Угол ∠AOB - центральный и равен 36°. Центральный угол измеряется дугой, на которую опирается. Следовательно, дуга AB = 36°.

Требуется найти длину дуги AB.

Зная радиус, можно найти длину окружности по формуле:

C = 2πR.

В данном случае длина окружности:

C = 2π·5 = 10π.

Так как длина окружности 360°, а дуга AB 36°, то видно, что дуга составляет 1/10 часть окружности (360° : 36° = 10).

Таким образом, длина дуги кругового сектора AB равна:

AB = 10π · 1/10 = π.