54. Длины сторон треугольника a, b и с находятся в зависимости а2 = b2 + с2 + √3·bc. Чему равен угол, лежащий против стороны а? |
|
A) |
125° |
B) |
150° |
C) |
135° |
D) |
140° |
| |
Правильный ответ:
|
B |
| |
Решение: |
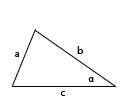
В данном случае требуется найти угол α, лежащий против стороны a. По теореме косинусов: а2 = b2 + с2 - 2·bc·cosα По условию задачи: а2 = b2 + с2 + √3·bc. Так как левые части равны (а2), следовательно, правые части тоже равны: b2 + с2 - 2·bc·cosα = b2 + с2 + √3·bc. Сокращаются b2 + с2: -2·bc·cosα = √3·bc. cosα = √3·bc : (-2·bc) = -√3/2. Угол α является тупым, т.к. его косинус отрицательный. cos30° = √3/2. cos(180° - 30°) = -√3/2. cos150° = -√3/2. Как видно, угол α равен 150°. |
| |
Категория: |
Геометрия |
|
В начало | Предыдущий | Следующий
|