52. AB||CD, OA = 3 см, OB = 4 см, AC = 2,25 см. Найти BD. 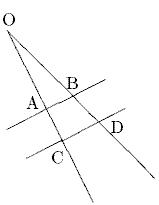
|
|
A) |
2,5 см |
B) |
2 см |
C) |
3 см |
D) |
2,1 см |
| |
Правильный ответ:
|
C |
| |
Решение: |
Стороны угла пересечены двумя параллельными прямыми AB и CD (по условию AB||CD). По теореме Фалеса: отрезки, высекаемые параллельными прямыми на одной прямой, пропорциональны отрезкам на другой прямой. 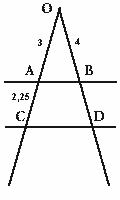
В данном случае отрезки OB и BD пропорциональны отрезкам OA и AC. Следовательно, получается пропорция: OA / AC = OB / BD. 3 / 2,25 = 4 / BD. Применим свойство пропорции, по которому произведение крайних членов равно произведению средних: 3 · BD = 2,25 · 4. 3 · BD = 9. BD = 9 / 3. BD = 3. |
| |
Категория: |
Геометрия |
|
В начало | Предыдущий | Следующий
|