23. Сколько целых решений имеет система неравенств:  3 - 4x > 5 3 - 4x > 5
2 + 3(x - 1) ≤ 4x + 5
|
|
A) |
1 |
B) |
2 |
C) |
4 |
D) |
6 |
| |
Правильный ответ:
|
D |
| |
Решение: |
Раскроем, где нужно, скобки и перенесем известные в одну сторону, неизвестные в другую, изменяя знаки на противоположные:  -4x > 5 - 3 -4x > 5 - 3
2 + 3x - 3 ≤ 4x + 5
 -4x > 2 -4x > 2
3x - 4x ≤ 5 - 2 + 3
 -x > 2/4 -x > 2/4
-x ≤ 6
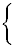 -x > 1/2 -x > 1/2
-x ≤ 6
Умножим обе части неравенств на -1, при этом знаки равенства изменятся на противоположные: 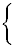 x < -1/2 x < -1/2
x ≥ -6
Как видно: -6 ≤ x < -1/2. Таким образом, целые решения данной системы неравенств: -6, -5, -4, -3, -2, -1. Всего целых решений 6. |
| |
Категория: |
Алгебра |
|
В начало | Предыдущий | Следующий
|