Воспользуемся формулой понижения степени косинуса:

cos2	α	=	1 + cosα
	2		2

Получаем:

4cos(x/2) + cosх + 1 = 4cos(x/2) + (1 + cosх) = 4cos(x/2) + 2cos²(x/2) = 2cos(x/2) · (2 + cos(x/2)) = 0, - здесь 2cos(x/2) вынесли за скобки.

Произведение равно нулю, если хотя бы один из множителей равен нулю, а другие при этом имеют смысл.

Поэтому (k ∈ Z):

а) 2cos(x/2) = 0.

cos(x/2) = 0.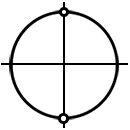

x/2 = π/2 + πk.

x = π + 2πk.

- при k = 0: x = π.

- при k = 1: x = π + 2π = 3π.

- при k = 2: x = π + 4π = 5π.

- при k = 3: x = π + 6π = 7π.

- при k = 4: x = π + 8π = 9π.

- при других значениях k корни не принадлежат промежутку [0; 9,5π].

б) 2 + cos(x/2) = 0.

cos(x/2) = -2.

Не имеет решений, т.к. -1 ≤ cosα ≤ 1 (т.е. косинус принимает значения только от -1 до 1 включительно).

Как видно, данное уравнение имеет 5 корней в промежутке [0; 9,5π].