1) Воспользуемся формулами приведения тригонометрических функций:

а) cos (π – α) = –cosα.

б) sin (π + α) = –sinα.

Учитываем, что функция y = cosx является четной, поэтому cos(х - π) = cos(π - x).

Получаем:

2(-cosх)² + 3sinх = 2cos²х + 3sinх = 3.

2) Заменим cos²х на (1 - sin²х) согласно основному тригонометрическому тождеству sin²х + cos²х = 1:

2·(1 - sin²х) + 3sinх - 3 = 0.

2 - 2sin²х + 3sinх - 3 = 0.

3) Примем sinх за t (|t| ≤ 1) и получим квадратное уравнение:

2t² - 3t + 1 = 0.

Дискриминант этого уравнения найдем по формуле: D = b² - 4ac = 9 - 4·2·1 = 1.

Корни уравнения найдем по формулам: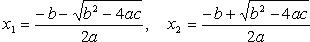

Получаем:

х₁ = (3 + 1)/4 = 1;

х₂ = (3 - 1)/4 = 1/2.

4) Как видно, уравнение имеет два корня. Таким образом:

а) sinx = 1;

x = π/2 + 2πk, k Є Z.

б) sinx = 1/2;

x = (-1)^k·arcsin1/2 + πk = (-1)^k·(π/6) + πk, k Є Z.