Знак тригонометрической функции зависит от координатной четверти, в которой располагается числовой аргумент.

Синус угла α — это ордината (координата y) точки на тригонометрической окружности.

Косинус угла α — это абсцисса (координата x) точки на тригонометрической окружности.

Тангенс угла α — это отношение синуса к косинусу. То есть отношение координаты y к координате x.

Котангенс - это отношение косинуса к синус. То есть отношение координаты x к координате y.

На рисунке ниже:

синим цветом обозначены положительные значения оси ординат (синус);

красным цветом - положительные значения оси абсцисс (косинус)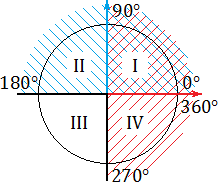

Как видно:

Синус в I и II четвертях положительный, в III и IV - отрицательный.

Косинус в I и IV четвертях положительный, во II и III - отрицательный.

Тангенс и котангенс в I и III четвертях положительные, во II и IV - отрицательные. Это следует из того, что тангенс является отношением синуса на косинус. В I четверти синус и косинус положительные, поэтому и тангенс положительный. Во II четверти синус положительный, но косинус отрицательный, поэтому и тангенс отрицательный (плюс на минус дает минус).

В данном случае учитываем, что каждые 360° можно отбросить, т.к. 360° составляют полный оборот. То есть через каждые 360° значения sinx, cosx, tgx, ctgx повторяются.

Кроме того, функции sin, tg, ctg являются нечетными, поэтому:

sin(-α) = -sinα,

tg(-α) = -tgα,

ctg(-α) = -ctgα.

Функция cos - четная, поэтому:

cos(-α) = cosα.

Следовательно, можно упростить расчеты:

а) sin(-910)° = -sin910° = -sin(910 - 360·2) = -sin(910 - 720) = -sin190°.

Угол 190° находится в III четверти, а так как sin в III и IV четвертях отрицательный, то -sin190° имеет знак плюс.

б) tg220°.

Угол 220° находится в III четверти, а так как tg в I и III четвертях положительный, то tg220° имеет знак плюс.

в) cos(-440)° = cos(440)° = cos(440 - 360) = cos80°.

Угол 80° находится в I четверти, а так как cos в I и IV четвертях положительный, то cos80° имеет знак плюс.

Следовательно, правильный порядок знаков

плюс, плюс, плюс.