8. Решите уравнение: 2cos4х + √2 = 0. |
|
A) |
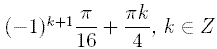
|
B) |
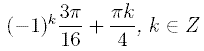
|
C) |
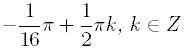
|
D) |

|
| |
Правильный ответ:
|
D |
| |
Решение: |
В данном случае воспользуемся формулой решения простейшего тригонометрического уравнения cosx = a: а) x = ±arccosa + 2πk, k ∈ Z (если a положительное число). б) x = ±(π - arccosa) + 2πk, k ∈ Z (если a отрицательное число). Преобразуем исходное уравнение: 2cos4x = -√2. cos4x = -√2/2. Применим вышеупомянутую формулу, учитывая, что a - отрицательное число: 4х = ±(π - arccos√2/2) + 2πk. 4х = ±(π - π/4) + 2πk. 4х = ±3/4π + 2πk. Обе части равенства разделим на 4, чтобы найти х: х = ±3/16π + πk/2. |
| |
Категория: |
Элементарная математика |
|
В начало | Предыдущий | Следующий
|