29. Найдите сумму корней уравнения: 
|
|
A) |
3 |
B) |
-4 |
C) |
-3 |
D) |
4 |
| |
Правильный ответ:
|
A |
| |
Решение: |
Для удобства расчетов перенесем правую часть в левую: 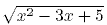 + х2 - 3х - 7 = 0. + х2 - 3х - 7 = 0.
Воспользуемся методом замены переменных: 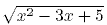 = t, t > 0. = t, t > 0.
Тогда: х2 - 3х + 5 = t2. Делаем замену: t + t2 - 5 - 7 = 0. Таким образом, квадратное уравнение относительно t имеет вид: t2 + t - 12 = 0. По теореме Виета: t1*t2 = -12. t1+t2 = -1. t1 = -4, t2 = 3. По вышеупомянутому условию t1 = -4 не подходит, т.к. t > 0. Остается t = 3. Следовательно: 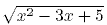 = 3. = 3.
х2 - 3х + 5 = 32 = 9. х2 - 3х -4 = 0. По теореме Виета: x1*x2 = -4. x1+x2 = 3. Как видно, сумма корней исходного уравнения равна 3. Доп. комментарий: Метод замены переменной заключается в том, что вместо сложного выражения вводится новая переменная, позволяющая сократить первоначальные расчеты. |
| |
Категория: |
Алгебра |
|
В начало | Предыдущий | Следующий
|