Параллелограмм - это четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению длин его сторон, умноженному на синус угла между ними: S = a · b · sinα. В данном случае угол ∠α составляет 60° по условию, а угол ∠ADB = 30°. 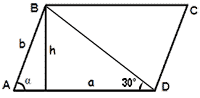
Следовательно, треугольник ADB прямоугольный, т.к. угол ∠ABD = 90°. Известно, что катет, лежащий против угла 30°, равен половине гипотенузы. Так как гипотенуза AD соответствует большой стороне параллелограмма (а) и по условию равна 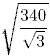 , то катет AB и, следовательно, меньшая сторона параллелограмма (b) составит: 1/2 · , то катет AB и, следовательно, меньшая сторона параллелограмма (b) составит: 1/2 · 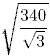 Вычислим по формуле площадь параллелограмма: S = a · b · sinα = 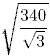 · 1/2 · · 1/2 · 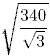 · sin60° = 340/√3 · 1/2 · √3/2 = 340/4 = 85. · sin60° = 340/√3 · 1/2 · √3/2 = 340/4 = 85. |