Медиана - это отрезок, который соединяет вершину треугольника с серединой противоположной стороны, т.е. делит эту сторону пополам.

В данном случае: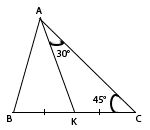

Так как медиана АК делит сторону ВС пополам, значит ВК = КС.

Очевидно, что искомое ВС равно двум КС (2·КС).

В треугольнике АКС имеем:

АК =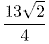

∠А = 30°

∠С = 45°.

Воспользуемся теоремой синусов, по которой стороны треугольника пропорциональны синусам противолежащих углов:

АК : sin45° = KC : sin30°.

KC = АК · sin30° : sin45° = AK · 1/2 : √2/2 = AK · 1/2 · 2/√2 = АК · 1/√2.

Вместо АК подставим :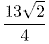

КС = 13√2/4 · 1/√2 = 13/4 = 3,25.

Так как ВС равно 2·КС, то ВС = 2·3,25 = 6,5.

Дополнительный комментарий:

Деление дробей можно заменить умножением, перевернув дробь-делитель:

1/2 : 2/3 = 1/2 · 3/2

1/2 : √2/2 = 1/2 : 2/√2.