Высота треугольника — это отрезок, опущенный из вершины треугольника перпендикулярно противоположной стороне.

Медиана - это отрезок, который соединяет вершину треугольника с серединой противоположной стороны, т.е. делит эту сторону пополам.

В данном случае: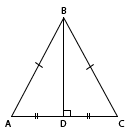

Треугольник ABC равнобедренный, значит боковые стороны AB и BC равны (AB = BC). Примем каждую из этих сторон за х (АВ = ВС = х).

Следовательно, основание АС составит (х + 6), т.к. основание на 6 больше боковой стороны.

Проведем высоту BD из вершины треугольника к основанию AC.

По условию задания BD = 6.

В равнобедренном треугольнике высота, проведенная из вершины, является медианой и биссектрисой.

Следовательно, основание AC делится на два отрезка по (x+6)/2.

В прямоугольном треугольнике ABD имеем:

катет BD = 6;

катет AD = (x + 6)/2;

гипотенузу АВ = х.

Воспользуемся теоремой Пифагора, по которой квадрат гипотенузы равен сумме квадратов катетов:

АВ² = BD² + AD².

Подставляем значения:

х² = 6² + (x + 6)²/2².

х² = 36 + (x + 6)²/4.

Умножим обе части уравнения на 4, чтобы избавиться от знаменателя:

4х² = 144 + (х + 6)².

Раскроем скобки по формуле квадрата суммы двух чисел:

4х² = 144 + х² + 12х + 36.

Перенесем все слагаемые в одну сторону:

4х² - х² - 12х - 180 = 0.

3х² - 12х - 180 = 0.

Разделим обе части на 3 для упрощения расчетов:

х² - 4х - 60 = 0.

По теореме Виета находим корни уравнения:

х₁ · х₂ = c/a = -60

х₁ + х₂ = -b/a = 4

Видно, что корнями уравнения являются:

х₁ = 10;

х₂ = -6.

Так как сторона треугольника не может быть отрицательной, то остается вариант х = 10.

Таким образом, искомое основание треугольника равно 10 + 6 = 16.