В данном случае углы треугольника относятся как 9:5:4, а сумма углов любого треугольника равна 180°.

Следовательно, можно найти величины этих углов.

Если принять одну часть за х, то углы составят 9х, 5х и 4х.

Сумма углов:

9х + 5х + 4х = 180°.

18х = 180°.

х = 10°.

Таким образом, величины углов:

90°, 50° и 40°.

Как видно, треугольник является прямоугольным (один из углов 90°).

БОльшая сторона треугольника лежит против бОльшего угла. В данном случае против угла 90°. БОльшей стороной, соответственно, является гипотенуза и медиана опущена именно к ней по условию задания.

В прямоугольном треугольнике медиана, опущенная на гипотенузу, равна половине гипотенузы.

Следовательно, гипотенуза AB в 2 раза больше медианы CD и равна 12,5 · 2 = 25.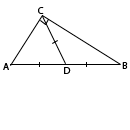