Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам. Радиус окружности — это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности. Радиус составляет половину диаметра. В данном случае: Радиус окружности OB = OA = 6. Диаметр окружности AB = 6 · 2 = 12, т.к. диаметр в два раза больше радиуса. 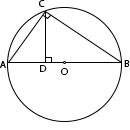
Так как по условию задачи перпендикуляр, опущенный из точки окружности C на диаметр, делит его в отношении 1:3, то диаметр разбивается на два отрезка AD = 3 и BD = 9 (1 + 3 = 4 части составляют длину диаметра 12, значит одна часть 12/4 = 3; вторая, соответственно, 3·3=9). Таким образом, получается прямоугольный треугольник ABC, где угол C является прямым (90°), т.к. опирается на диаметр и измеряется половиной дуги AB (180°). CD является высотой треугольника ABC. AD является проекцией катета AC, а BD - проекцией катета BC на гипотенузу. Используем теорему, по которой CD есть среднее пропорциональное между проекциями AD и BD. Получаем: AD : CD = CD : BD. 3 : CD = CD : 9. Воспользуемся свойством пропорции, по которому произведение крайних членов пропорции равно произведению средних: CD · CD = 3 · 9. CD2 = 27. CD = 3√3. |