Признаки равенства двух треугольников:

I. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.

II. Если сторона и прилежащие к ней углы одного треугольника равны соотвественно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

III. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Треугольник называется равнобедренным, если у него две стороны равны.

Равные стороны называются боковыми, а третья сторона называется основание треугольника.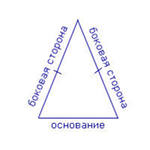

У равнобедренного треугольника углы при основании равны.

Медиана - это отрезок, который соединяет вершину треугольника с серединой противоположной стороны, т.е. делит эту сторону пополам.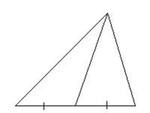

Медиана, проведенная к основанию треугольника, является биссектрисой, т.к. делит угол пополам, и высотой, т.е. перпендикуляром, опущенным из вершины треугольника на противоположную сторону, или на ее продолжение.

В любом треугольнике медианы в точке их пересечения делятся в отношении 2:1, считая от вершины.

Равносторонний треугольник - это треугольник, у которого все стороны равны.

В равностороннем треугольнике все углы по 60°.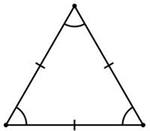

В равностороннем треугольнике любая медиана является высотой и биссектрисой.

Все три медианы в любом треугольнике пересекаются в одной точке.

То же самое касается и высот, и биссектрис.

В остроугольном треугольнике, где все углы острые, т.е. меньше 90°, точка пересечения высот лежит внутри треугольника.

В тупоугольном треугольнике, где один из углов тупой, т.е. лежит в пределах между 90° и 180°, точка пересечения высот лежит вне треугольника.

В прямоугольном треугольнике, где один из углов прямой, т.е. равен 90°, точка пересечения высот лежит на середине гипотенузы и является центром описанной окружности.

Сумма углов треугольника равна 180°.

Сумма внешних углов любого многоугольника равна 360°.

Сумма внутренних углов выпуклого многоугольника (n-угольника) определяется по формуле:

180° · (n - 2).

При пересечении двух параллельных прямых третьей прямой (секущей) образуются следующие углы: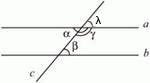

а) Внутренние накрест лежащие углы, расположенные во внутренней области параллельных прямых и на разных сторонах секущей. Внутренние накрест лежащие углы равны.

На рисунке это углы α и β.

б) Соответственные углы, лежащие на одной стороне секущей, один из которых расположен во внешней области, а другой - во внутренней области. Соответственные углы равны.

На рисунке это углы β и λ.

в) Внутренние односторонние углы - это углы, лежащие на одной стороне секущей и расположенные во внутренней области. Сумма внутренних односторонних углов равна 180°.

На рисунке это углы β и γ.

В данном случае:

1) Сумма внутренних односторонних углов при пересечении двух параллельных прямых третьей прямой составляет ровно 180°. Следовательно, утверждение неверно.

2) В равностороннем треугольнике высоты являются одновременно и медианами, а медианы в любом треугольнике в точке их пересечения делятся в отношении 2:1, считая от вершины. Следовательно, утверждение неверно.

3) Так как сумма острых углов прямоугольного треугольника равна 90° (180° минус прямой угол 90°), то второй острый угол одного треугольника равен второму острому углу другого треугольника в данном случае. Следовательно, такие треугольники равны по одной стороне и прилежащим к ней углам. Утверждение верно.

4) Ни к одному из признаков равенства треугольников данное утверждение не подходит. Следовательно, оно неверно.

Как видно, верным является утверждение "два прямоугольных треугольника равны, если имеют равные гипотенузы и по одному равному острому углу".