21. Найдите |x - y|, если: 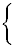 x2 + y2 = 89 x2 + y2 = 89
x + y = 3
|
|
A) |
13 |
B) |
14 |
C) |
6 |
D) |
11 |
| |
Правильный ответ:
|
A |
| |
Решение: |
Возведем обе части второго равенства в квадрат: 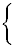 x2 + y2 = 89 x2 + y2 = 89
(x + y)2 = 32
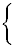 x2 + y2 = 89 x2 + y2 = 89
x2 + y2 + 2xy = 9
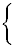 x2 + y2 = 89 x2 + y2 = 89
89 + 2xy = 9
 x2 + y2 = 89 x2 + y2 = 89
2xy = -80
Возведем (x - y) в квадрат: (x - y)2 = x2 + y2 - 2xy = 89 - (-80) = 89 + 80 = 169. Таким образом: (x - y) = √169 = ±13. Так как требуется найти модуль |x - y|, который всегда положителен, то остается вариант 13. |
| |
Категория: |
Алгебра |
|
В начало | Следующий
|