Для удобства расчетов заменим sinх на t и получим квадратное уравнение (причем -1 ≤ t ≤ 1, т.к. синус принимает значения только от -1 до 1 включительно):

t² - 5/2 t + 1 ≤ 0.

Умножим обе части на 2, чтобы избавиться от дробей:

2t² - 5t + 2 ≤ 0.

Решим методом интервалов.

Найдем нули выражения 2t² - 5t + 2:

Дискриминант вычислим по формуле D = b² - 4ac:

D = (-5)² - 4·2·2 = 25 - 16 = 9.

Нули найдем по формулам: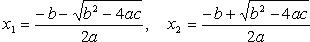

Получаем:

t₁ = (5 - √9) / 2·2 = (5 - 3) / 4 = 2/4 = 1/2.

t₂ = (5 + √9) / 2·2 = (5 + 3) / 4 = 8/4 = 2.

Отметим полученные нули на числовой оси. Получается 3 интервала:

(-∞; 0,5) U (0,5; 2) U (2; ∞).

Круглые скобки означают, что концы не входят в интервал.

Выражение 2t² - 5t + 2 меньше нуля на интервале (0,5; 2).

На остальных интервалах значения выражения больше нуля и не являются решением неравенства.

Так как выше обозначили, что -1 ≤ t ≤ 1, то интервал сужается до (0,5; 1].

Так как sinx ≤ 1 верно при всех х ∈ R, то рассмотрим только sinx > 0,5.

Для этого на единичной окружности проведем прямую y = 0,5 = 1/2 параллельно оси абсцисс.

Прямая пересечет окружность в двух точках:

P₁ = arcsin 1/2 = π/6;

P₂ = π - π/6 = 5π/6.

Неравенству sinx > 0,5 удовлетворяют лишь точки меньшей дуги (где 0,5 < х ≤ 1 на оси ординат).

В условии требуется найти углы из промежутка [0; 2π], т.е. от 0° до 360°.

Углы меньшей дуги соответствуют (π/6; 5π/6) (от 30° до 150°, исключая концы).

Таким образом, неравенство верно при х Є (π/6; 5π/6).