В данном случае применяется формула квадрата суммы двух выражений:

(a + b)² = a² + 2ab + b².

Также учитываем, что (√a)² = a; например, (√9)² = 3² = 9.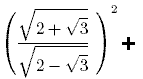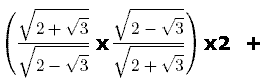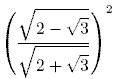

Применим формулу разности квадратов:

(a - b)(a + b) = a² - b².

Таким образом:

(2 + √3) · (2 - √3) = 4 - 3 = 1.

Получаем:

(2 + √3) / (2 - √3) + 2·√1/√1 + (2 - √3) / (2 + √3) - 2 = (2 + √3) / (2 - √3) + (2 - √3) / (2 + √3).

Приведем к общему знаменателю (2 + √3)(2 - √3) = 1 (см. выше формулу разности квадратов):

(2 + √3)² / 1 + (2 - √3)² / 1 = (2 + √3)² + (2 - √3)².

Раскроем скобки, используя упомянутую выше формулу квадрата суммы двух выражений:

2² + 2·2·√3 + √3² + 2² - 2·2·√3 + √3² = 4 + 3 + 4 + 3 = 14.