Центральный угол окружности измеряется дугой, на которую опирается.

В данном случае:

центральный угол АОВ измеряется дугой АВ,

центральный угол ВОС - дугой ВС,

центральный угол АОС - дугой AmC.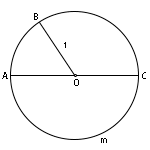

Центральные углы пропорциональны числам 1, 2 и 3, поэтому, если принять дугу АВ за х, то:

дуга ВС = 2х,

дуга AmC = 3x.

Длина окружности составляет 2πR = 2π·1 = 2π (R = 1 по условию).

Сложив все дуги, получим длину окружности:

х + 2х + 3х = 2π.

6х = 2π.

х = 2π : 6 = π/3.

Так как требуется найти наибольшую дугу AmC, то она составляет:

AmC = 3х = 3 · π/3 = π.